Расчет стойки на прочность и устойчивость: онлайн

Онлайн калькулятор для расчёта стойки (колонны) из стального проката

Логика онлайн расчета на прочность и устойчивость стойки из стального проката

Согласно Актуализированной редакция СНиП II-23-81 (CП16.13330, 2011) рассчитывая на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:

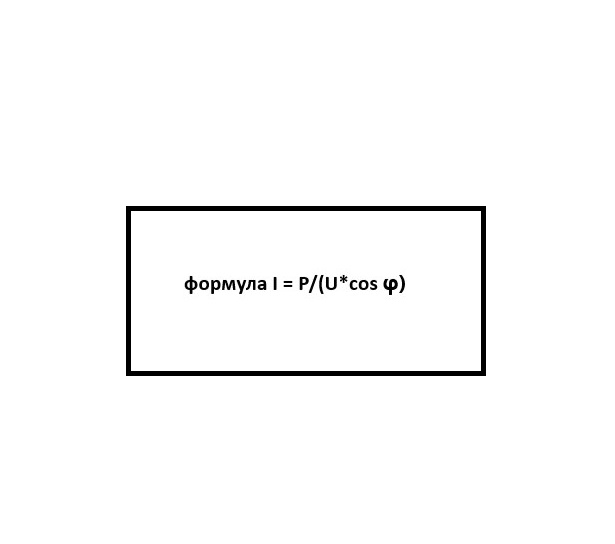
P / Fp * Ry * Yc <= 1

• где P – действующая нагрузка.
• Fp – площадь поперечного сечения колонны.
• Ry – подсчетное сопротивление материала (стали колонны), выбирается по таблице В5 Приложения “В” того же СНиПа.
• Yc – коэффициент условий работы по таблице 1 СНиПа (0.9-1.1). В соответствии с примечанием к этой таблице (пункт 5) в калькуляторе принято Yc=1.

Проверку на устойчивость элементов сплошного сечения при центральном сжатии силой P следует выполнять по формуле:

P / Fi * Fp * Ry * Yc <= 1

где Fi – коэффициент продольного изгиба центрально – сжатых элементов.

Коэффициент Fi введён в качестве компенсации возможности некоторой не прямолинейности колонны, недостаточной жесткости её крепления и неточности в приложении нагрузки относительно оси стойки.

Значение Fi зависит от марки стали и гибкости колонны и часто берётся из таблицы 72 СНиП II-23-81 1990г., исходя из гибкости колонны и расчётного сопротивления выбранной стали сжатию, растяжению и изгибу.

Это несколько упрощает и огрубляет вычисления, так как СНиП II-23-81* предусматривает специальные формулы для определения Fi. Гибкость (Lambda) – некоторая величина, характеризующая свойства рассматриваемого стержня в зависимости от его длины и параметров поперечн. сечения, в частности радиуса инерции:

Lambda = Lr / i

• здесь Lr – расчётная длина стержня,
• i – радиус инерции поперечного сечения стержня (колонны).

Радиус инерции сечения i равен корню квадратному из выражения I / Fp, где I – момент инерции, Fp – его площадь.

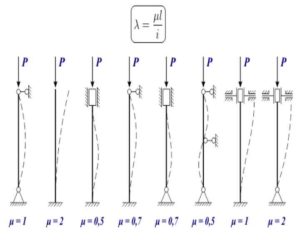
Lr (расчётная длина) определяется как Mu*L; здесь L – длина стойки, а Mu – коэфф., зависящий от схемы её крепления:

• “заделка-консоль”(свободный конец) – Mu=2;
• “заделка-заделка” – Mu = 0.5;
• заделка – шарнир” – Mu = 0.7;
• “шарнир – шарнир” – Mu = 1.

Следует иметь ввиду,что при наличии у формы поперечн. сечения 2-ух радиусов инерции (например, у прямоугольника), при вычислении Lambda используется меньший.

Для их использования необходимо сделать выбор в таблице онлайн калькулятора “Вид, назначение стоек”. Предельная гибкость стоек, кроме их геометрических параметров, зависит также от коэффициента продольного изгиба (Fi), действующей нагрузки (P), расчётного сопротивления материала стоики (Ry) и условий её работы (Yc).

Предельная гибкость, устойчивость и прочность стоек, кроме их геометрических параметров, зависит также от коэффициента продольного изгиба (Fi), действующей нагрузки (P), расчётного сопротивления материала стойки (Ry) и условий её работы (Yc).

Если возникнут трудности при расчетах онлайн калькулятором прочности и устойчивости, рекомендуем предварительно ознакомиться с инструкцией.

Метрология гибкости[править | править код]

Гибкость — это способность выполнять движения с большой амплитудой. Термин «гибкость» подразумевает под собой суммарную подвижность в суставах всего тела. Применительно же к отдельным суставам принято употреблять понятие «подвижность». К примеру, «подвижность в коленных суставах».

По форме проявления различают активную и пассивную гибкость.

Активная гибкость подразумевает выполнение движения с большой амплитудой за счёт собственной активности соответствующих мышц. Она зависит от состояния ЦНС и волевых усилий. Существенное влияние на проявление активной гибкости также оказывает возбудимость растягиваемых мышц, которая препятствует чрезмерному растяжению мышечных волокон.

Пассивная гибкость — это способность выполнять движения с большой амплитудой под воздействием внешних сил: внешнего отягощения, усилий партнёра, специальных приспособлений и т.п.. Она зависит от формы суставных костей, эластичности мышц, связок и сухожилий. Пассивная гибкость всегда выше активной.

По способу проявления выделяют динамическую и статическую гибкость. Первая проявляется в движениях, а вторая — при удержании определённой позы.

Кроме того, в теории спорта принято выделять общую и специальную гибкость. Общая гибкость определяется высокой подвижностью во всех суставах тела, а специальная гибкость — амплитудой движений, характерной для техники конкретного двигательного действия.

Факторы, влияющие на гибкостьправить | править код

Основное влияние на проявление гибкости оказывает ряд факторов:

анатомический — кости являются ограничителями движений; их форма определяет направление и размах движений в суставе (сгибание, разгибание, отведение, приведение, пронация, супинация, вращение);

центрально-нервная регуляция тонуса мышц и межмышечная координация — способность произвольно расслаблять растягиваемые и напрягать, осуществляющие движение, мышцы.

Существенное влияние на проявление гибкости оказывают также внешние условия:

время суток — днём и вечером (12-17 часов) гибкость выше, нежели утром;

температура окружающей среды — к примеру, при 5-10 °С гибкость ниже, чем при 20-30 °С;

разминка — после разминки гибкость повышается;

температура тела — например, подвижность в суставах увеличивается после 10 минут пребывания в сауне).

Функциональное состояние организма тоже способно оказывать влияние на подвижность суставов. Так, утомление способствует уменьшению активной гибкости (ввиду снижения способности мышц к полному расслаблению после предшествующего сокращения) и повышению пассивной (ввиду пониженного тонуса мышц, противодействующих растяжению).

Кроме всего перечисленного, мотивация и положительные эмоции повышают гибкость, а негативные личностно-психические факторы снижают.

Основные сведения

У стержней, длина которых значительно больше поперечных размеров, при определенной величине осевой сжимающей силы происходит искривление оси. Это явление носит название продольного изгиба. Переход прямолинейной формы равновесия в криволинейную называется потерей устойчивости.

Сжимающая сила, при которой прямолинейная форма равновесия перестает быть устойчивой, называется критической. Ее можно определить по формуле Эйлера

где Е – модуль продольной упругости материала;
l – длина стержня;
I_min – минимальный момент инерции сечения;μ – коэффициент приведения длины, который зависит от способов закрепления концов стержня.

Формула Эйлера применима лишь в том случае, если потеря устойчивости стержня происходит при напряжениях, меньших предела пропорциональности σ_пц, т.е. когда справедлив закон Гука

Здесь А – площадь поперечного сечения;λ=μ∙l/i_min – гибкость стержня;
– минимальный радиус инерции сечения.

Предельная гибкость, начиная с которой можно использовать формулу Эйлера, определяется по формуле

зависит лишь от физико-механических свойств и является постоянной для данного материала.
Так, например, для стали Ст.З λ_пр = 100, для древесины λ_пр = 110, для чугуна λ_пр = 80, для дюралюминия λ_пр = 60.

Стержни, у которых λ > λ_пр, называются стержнями большой гибкости.

При меньших значениях гибкости (стержни средней гибкости) критические напряжения σ_кр > σ_пц определяются по эмпирическим формулам или соответствующим им таблицам (графикам). Например, формула Ясинского для определения критических напряжений имеет вид

σ_кр = a – bλ,     (14.4)

где a и b – эмпирические коэффициенты.
Например, для стали Ст.3 a = 310 МПа, b = 1,14 МПа, для древесины (сосна) a = 28,7 МПа, b = 0,19 МПа.

Эмпирические формулы, особенно для древесины, дают лишь приближенный результат.

Для стержней малой гибкости, у которых σ_кр, подсчитанные по формуле Ясинского, получаются больше, чем опасные (предельные) напряжения, принимают:σ_кр = σ_т – для пластичных материалов;σ_кр = σ_пч – для хрупких материалов.

Расчет внецентренно-сжатой колонны.

Тут конечно же возникает вопрос: а как рассчитать остальные колонны, ведь нагрузка к ним будет приложена скорее всего не по центру сечения? Ответ на этот вопрос сильно зависит от способа крепления навеса к колоннам. Если балки навеса будут жестко крепиться к колоннам, то при этом будет образована достаточно сложная статически неопределимая рама и тогда колонны следует рассматривать как часть этой рамы и рассчитывать сечение колонн дополнительно на действие поперечного изгибающего момента, мы же далее рассмотрим ситуацию когда колонны, показанные на рисунке 1, соединены с навесом шарнирно (колонну, обозначенную красным цветом, мы больше не рассматриваем). Например оголовок колонн имеет опорную площадку — металлическую пластину с отверстиями для болтового крепления балок навеса. По разным причинам нагрузка на такие колонны может передаваться с достаточно большим эксцентриситетом:

Рисунок 2. Эксцентриситет приложения сосредоточенной нагрузки к колонне из-за прогиба балки навеса.

Балка, показанная на рисунке 2, бежевым цветом, под воздействием нагрузки немного прогнется (почему это произойдет, обсуждается отдельно) и это приведет к тому, что нагрузка на колонну будет передаваться не по центру тяжести сечения колонны, а с эксцентриситетом е и при расчете крайних колонн этот эксцентриситет нужно учитывать. Более точное определение эксцентриситетов зависит от жесткости колонны и балки, но мы в данном случае не будем учитывать жесткости и для надежности примем максимально неблагоприятное значение эксцентриситета. Случаев внецентренного нагружения колонн и возможных поперечных сечений колонн существует великое множество, описываемое соответствующими формулами для расчета. В нашем случае для проверки сечения внецентренно-сжатой колонны мы воспользуемся одной из самых простых:

(N/φF) + (M_z/W_z) ≤ R_y (3.1)

Т.е. предполагается, что внецентренное нагружение имеется только относительно одной оси.

В данном случае, когда сечение самой нагруженной колонны мы уже определили, нам достаточно проверить, подходит ли такое сечение для остальных колонн по той причине, что задачи строить сталелитейный завод у нас нет, а мы просто рассчитываем колонны для навеса, которые будут все одинакового сечения из соображений унификации.

Что такое N, φ и R_y мы уже знаем.

Формула (3.1) после простейших преобразований, примет следующий вид:

F = (N/R_y)(1/φ + e_z·F/W_z) (3.2)

так как максимально возможное значение изгибающего момента М_z = N·e_z, почему значение момента именно такое и что такое момент сопротивления W, достаточно подробно объясняется в отдельной статье.

Сосредоточенная нагрузка N на колонны, обозначенные на рисунке 1 синим и зеленым цветом, составит 1500 кг. Проверяем требуемое сечение при такой нагрузке и ранее определенном φ = 0.425

F = (1500/2050)(1/0.425 + 2.5·3.74/5.66) = 0.7317·(2.353 + 1.652) = 2.93 см2

Кроме того, формула (3.2) позволяет определить максимальный эксцентриситет, который выдержит уже рассчитанная колонна, в данном случае максимальный эксцентриситет составит 4.17 см.

Требуемое сечение 2.93 см2 меньше принятого 3.74 см2, а потому квадратную профильную трубу с размерами поперечного сечения 50х50 мм с толщиной стенки 2 мм можно использовать и для крайних колонн.

Примечание: Вообще-то изгибающий момент от эксцентриситета в наиболее опасном сечении, расположенном примерно посредине высоты колонны, будет в 2 раза меньше, соответственно и требуемая площадь сечения тоже будет немного меньше. Но как я уже говорил, при выполнении расчета не специалистом дополнительный запас по прочности никогда не помешает. К тому же в данном случае мы все равно принимаем большую площадь сечения из конструктивно-эстетических соображений.

Приложение I

Нагрузки и коэффициенты перегрузки

Таблица: Нормативные и расчетные нагрузки, коэффициенты перегрузки

Таблица: Нормативные и расчетные нагрузки, коэффициенты перегрузки (продолжение)

Коэффициенты условий работы m

Коэффициенты условий работы для стальных конструкций при расчете их по несущей способности должны приниматься:

• Для элементов конструкций (m):
  • для корпусов и днищ резервуаров — 0,8
  • для колонн гражданских зданий и опор водонапорных башен — 0,9
  • для сжатых элементов ферм и для сплошных балок перекрытий под залами театров, клубов, кино, трибун, помещений магазинов, книгохранилищ и архивов при весе перекрытий, равном или большем полезной нагрузки — 0,9
  • для сжатых элементов стропильных ферм и для прогонов кровель зданий при снеговой нагрузке не более 70 кг/м2 и весе кровли 150 кг/м2 и более, а также при снеговой нагрузке не более 100 кг/м2 и весе кровли 300 кг/м2 и более — 0,95
  • для элементов, прикрепляемых односторонне (равнобоких уголков и неравнобоких, прикрепляемых узкой полкой) — 0,75
• Для соединений конструкций (m_с):
  • для заклепок с потайными или полупотайными головками — 0,8
  • для заклепок, работающих на растяжение (отрыв головок) — 0,6
  • для черных, чистых и рифленых болтов, работающих на растяжение — 0,8
  • для анкерных болтов, работающих на растяжение — 0,65
• Для прочих элементов конструкций и соединений (за исключением указанных в примечании и в специальных технических условиях) — 1

Примечание. Коэффициенты условий работы листовых конструкций доменных цехов, силосов и бункеров, а также мачт электропередач устанавливаются специальными техническими условиями.

Пошаговая инструкция проведения расчета

1.Вводят тип проката: круглый, квадратный, в форме полосы, шестигранника и т.д.

2.Указывают разновидность схемы, по которой крепится стойка: в виде заделки консоли, в виде заделки заделки, в виде заделка шарнир, либо шарнир шарнир.

3.Выбирают материал проката, к примеру: из Стали С235 — Ст3кп2, из Стали С245 — Ст3пс5 либо Ст3сп5.

4.Устанавливают разновидность стойки, ее назначение, к примеру: стойки передающие, служащие для опоры, основные либо второстепенные.

Важно! При отсутствии типа материала в таблице, а показатель его расчетного сопротивления (кг /см 2) известен, значит, следует ввести значение в специальное поле. Чтобы произвести расчет вводят:

Чтобы произвести расчет вводят:

1.Длину стойки — L, выражают в метрах.

2.Размер D либо Dv, либо A, выражают в миллиметрах.

3.Размер B, выражают в миллиметрах.

4.Нагрузку на колонну — P, выражают в килограммах.

По последней версии СНиПа II – 23 – 81 проводя расчет прочности стальных деталей, оснащенных центральным растяжением либо сжатием посредством силы Р вычисляют при помощи следующей формулы:

P : Fp Х Ry Х Yc<=1

Расчет на устойчивость детали, имеющей сплошное сечение с центральным сжатием силой Р вычисляют согласно формуле:

P : Fi х Fp х Ry х Yс<=1

В формуле:

1.Fi – значение коэффициента, указывающий на продольный изгиб, элементов центрально – сжатого типа.

Данный коэффициент компенсирует небольшую не прямолинейность стойки, нехватку крепежной жесткости, также неточность определения нагрузки вдоль двух осей колонны.

Параметр Fi отличается в зависимости от марки стального материла его гибкости, как правило, значение определяют по таблице No 72 из СНиПа II-23-81 за 1990 год, зависит также от показателя сопротивления материала, сжатию при расчете, изгиба и растяжения.

Данное условие делает расчет более простым, но более грубым, потому что в СНиП указаны инженерные формулы, по которым рассчитывают Fi.

Физическая величина – гибкость стойки, по-другому Lambda, определяющая параметры стойки, которые значение длины, поперечное сечение, в том числе значение инерционного радиуса.

LAMBDA = Lr : i

В формуле:

Lr – значение расчётной стержневой длины.

i – значение инерционного радиуса стержневого диаметра поперечного типа.

Данная величина, обозначаемая i вычисляется, как корень квадратный из значения I : Fp, в котором I равен моменту инерции, а Fp равно площади сечения.

Lr=Mu * L,

В формуле:

Mu – коэффициент, определяемый крепежной схемой колонны.

L – значение длины стойки.

Важно! Если у прямоугольника, имеющего два радиуса инерции сечения, вычисляют Lambda, использовать следует наименьший из них. Гибкость стойки, которую рассчитывают по вышеуказанной схеме, не может быть выше значения 220 согласно таблице No 19 по СНиПу II – 23 – 81, в нем указаны максимальные показатели предельной гибкости стоек центрально-сжатого типа

Гибкость стойки, которую рассчитывают по вышеуказанной схеме, не может быть выше значения 220 согласно таблице No 19 по СНиПу II – 23 – 81, в нем указаны максимальные показатели предельной гибкости стоек центрально-сжатого типа.

Чтобы их правильно применять, следует в калькуляторе выбрать таблицу с названием Вид и назначение стоек, далее определить подвид.

Значение предельной гибкости определяется параметрами геометрических фигур, на величину влияет изгиб продольный, нагрузка, расчетное сопротивление материала изделия, рабочие условия.

Перед тем, как начать работать в калькуляторе онлайн, следует тщательно изучить инструкцию.

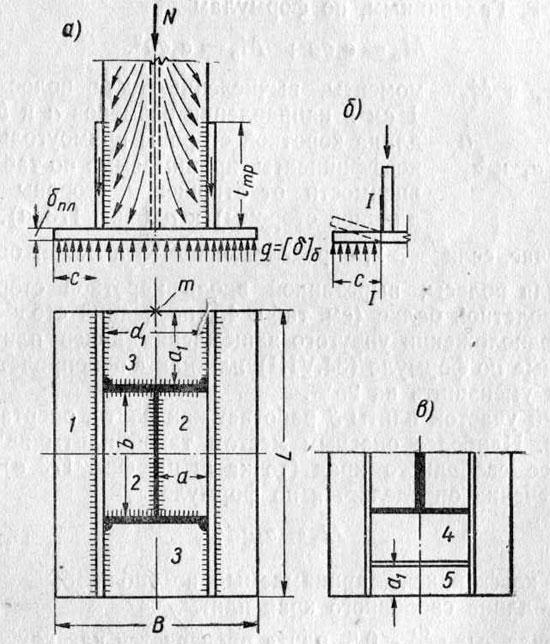
7.4 Прочность и устойчивость сквозных стержней

7.4.1 Сквозные
стержни с решёткой, нагруженные продольными и поперечными силами, а также
моментами, рассчитываются как конструкции (суперэлементы), а для проверяемых
элементов производится проверка их несущей способности и долговечности.

7.4.2 Сквозные
стержни на планках работают в условиях близких к продольному центральному
сжатию. При таком нагружении планки оказываются нагруженными перерезывающими
силами за счёт эксцентриситетов приложенных продольных сил. При этом одна
половина планки работает как консольный стержень, её расчётная схема показана
на , где:

L — длина сквозного стержня;

b— поперечный размер сквозного стержня;

n— число планок в одной грани сквозного стержня;

λ — гибкость сквозного стержня;

— деформация текучести;

e и е₁— эксцентриситеты приложения встречных сил на концах
сквозного стержня, на рисунке 7.2 эксцентриситеты показаны положительными;

N- сжимающие силы, действующие по одной линии;

Q — перерезывающая сила, приложенная к среднему сечению планки;

— минимальная безразмерная стрелка начальной погиби,
при наличии технических условий значение может быть принято
иным.

Рисунок 7.2 — Расчетная схема планки сквозного стержня

7.4.3 Величина
перерезывающей силы определяется по формуле:

(7.9)

При или при
неопределённых эксцентриситетах принимается минимальное значение перерезывающей
силы:

(7.10)

В соответствии
с принятой расчётной схемой вычисляются геометрические размеры планки как
консольного стержня и сварных швов прикрепления планки к поясу (см. ).

7.4.4 Проверка
устойчивости сквозного стержня в целом осуществляется следующим образом:
рассчитывается несущая способность второй (слабой , ) ветви стержня в
пределах панели N_п, а затем вычисляется несущая способность
стержня в целом.

В пределах
следующих диапазонов:

,

λ₂
= 20÷80 гибкость второй (слабой) ветви в пределах панели, суммарная
несущая способность центрально сжатого сквозного стержня определяется по
формуле:

(7.11)

где:

суммарная площадь сечения обоих
ветвей;

— отношение площадей поперечных сечений
ветвей;

— отношение усилий в ветвях в критическом
состоянии;

— коэффициент снижения расчётного
сопротивления, зависящий от вида поперечного сечения ветвей.

На
рисунке 7.3 показаны два типа сечений сквозных стержней с тавровым и различными
сечениями второй ветви и приведены соответствующие значения коэффициентов k и ζ,.

Рисунок 7.3 — Сечения сквозных стержней

Зависимость для крайних значений k =
1 и k = 2 дана в таблице 7.5,

для
промежуточных значений kи λ,
величина β определяется при помощи линейной интерполяции.

Таблица
7.5

λ
k= 1	k = 2
20	0.921	0.927
40	0.857	0.863
60	0.766	0.778
80	0.620	0.653
100	0.402	0.484
120	0.140	0.308
140	-0.0905	0.149
160	-0.271	0.0230

Порядок выполнения и обработка результатов

Опыты по исследованию устойчивости сжатых стержней производятся либо на испытательных машинах малой мощности (Р-5 и других), либо на специальных установках, например, СМ-20.

На испытательных машинах величина критической силы определяется непосредственно по шкале динамометра.

На установке СМ-20 (рис. 14.1) нагружение производится с помощью винтовой пары (подъемный винт-гайка) через тарированную пружину; величина нагрузки определяется по осадке пружины δ, которая пропорциональна сжимающей силе:

F = С · δ,

где С – жесткость пружины, определяется из тарировочного графика.

Рис. 14.1. Схема установки СМ-20:

1 – образец; 2 – корпус; 3 – верхняя опора;
4 – ограничительные упоры;
5 – нижняя опора; 6 –силовое устройство

Установка СМ-20 позволяет определить критическую силу для стержня с шарнирно опертыми концами (μ = 1).

Порядок проведения испытаний и обработки результатов следующий.

1. Измеряем длину и размеры поперечного сечения образца, определяем геометрические характеристики сечения и гибкость стержня (I_min, A, i_min, λ).
2. Сравниваем значения λ и λ_пр, выясняем, по какой формуле следует определять критическую силу.
3. Вычисляем теоретическое значение критической силы.
4. Устанавливаем стержень на опорах установки.
5. Упоры при помощи винтов устанавливаем примерно на одинаковых расстояниях (2 – З мм) от испытуемого образца.
6. Производим нагружение стержня путем плавного и медленного вращения маховика по часовой стрелке, с возрастанием нагрузки нужно непрерывно следить за поведением образца.
   Если при F < F_кр слегка изогнуть стержень рукой и отпустить, после некоторых колебаний он вновь выпрямится (устойчива прямолинейная форма равновесия).
   С увеличением нагрузки частота собственных колебаний уменьшается, и при критической нагрузке она равна нулю.
   При достижении нагрузкой критического значения стержень слегка искривляется и касается одного из упоров. Если изогнутый стержень руками вернуть в исходное прямолинейное положение и отпустить, он вновь искривится, т.е. прямолинейная форма перестала быть устойчивой.
7. Снимаем отсчет по шкале осадки пружины δ и заносим его в журнал испытаний, разгружаем образец вращением маховика против часовой стрелки.
8. Определяем по паспорту установки коэффициент жесткости пружины С.
9. Вычисляем опытное значение критической силы
   F_{кр оп}= С · δ.
10. Сравниваем величины F_{кр оп} и F_{кр т}, определяем процент расхождения и делаем соответствующие выводы.